Written by Deven Joshi
One of the most powerful widgets in the Flutter catalog (and for me, one
of the most underrated) is the Transform widget. Transform widgets allow
us to fundamentally alter how widgets look and behave, allowing us to
create new, complex types of animations. Underneath the Transform
widget, a 4D matrix powers the actual transformation — defined by the
Matrix4 class. While Flutter provides easy ways to do transformations
such as translation, scaling, and rotation, we can use the Matrix4 to
create even more awesome things such as 3D perspective transformation.
In this article, we are going to explore the 4D matrix itself and what
the individual values in it do. In the previous Transform Deep
Dive
I wrote, we discussed how to use Transforms without directly interacting
with a 4D matrix. Check it out if you need a refresher on the easier
uses of the widget.
What is a 4D matrix?
Even though anything with “4D” attached to it sounds cool by default, in
reality, a 4D matrix is simply a matrix with 4 rows and 4 columns. We
need to use a 4D matrix to transform an object in 3 dimensions (Here,
the dimensions are what we’re used to: length, breadth and height).
This formation of the matrix is called an identity matrix. The best
way to think of an identity matrix is that this is the equivalent of the
number ‘1’ in the matrix form — It leaves things untouched when used
to transform widgets.
Using different combinations of numbers in this matrix, we can
manipulate the shape, size, orientation, etc of a given object.
Let’s look at how we do this.
Basic Setup
Let’s take a look at the code that we are going to use for
experimentation:
class MyHomePage extends StatefulWidget {
@override
_MyHomePageState createState() => _MyHomePageState();
}
class _MyHomePageState extends State<MyHomePage> {
double x = 0;
double y = 0;
double z = 0;
@override
Widget build(BuildContext context) {
return Scaffold(
body: Center(
child: Transform(
transform: Matrix4(
1,0,0,0,
0,1,0,0,
0,0,1,0,
0,0,0,1,
)..rotateX(x)..rotateY(y)..rotateZ(z),
alignment: FractionalOffset.center,
child: GestureDetector(
onPanUpdate: (details) {
setState(() {
y = y - details.delta.dx / 100;
x = x + details.delta.dy / 100;
});
},
child: Container(
color: Colors.red,
height: 200.0,
width: 200.0,
),
),
),
),
);
}
}
The code simply uses a Transform widget and a colored Container to
transform. We define an identity Matrix4 for the starting point which
does… well.. nothing at all. The rest of the code with the
GestureDectector allows us to rotate the square in X and Y directions.
The code for rotating the square is final and we do not intend to make
any changes to it. If you need more information on what we’re doing, I
suggest looking at Wm Leler’s article on
Perspective in Flutter where
a similar method is used. The x, y, and z variables simply track the
amount of rotation that has already been done.
We will come back to why we’re allowing the user to rotate the square
later, for now, we focus on the matrix and basic 2D results.
Note 1: The line
alignment: FractionalOffset.center,
sets the centre of the transformation to the centre of the square.
Note 2 (for nerds): Matrix4 is in column-major order by default. In
the way the code is written, we effectively write it in row-major
format. Hence, all the row and column values written will be inverted
along the diagonal.
Here’s how the screen looks right now:
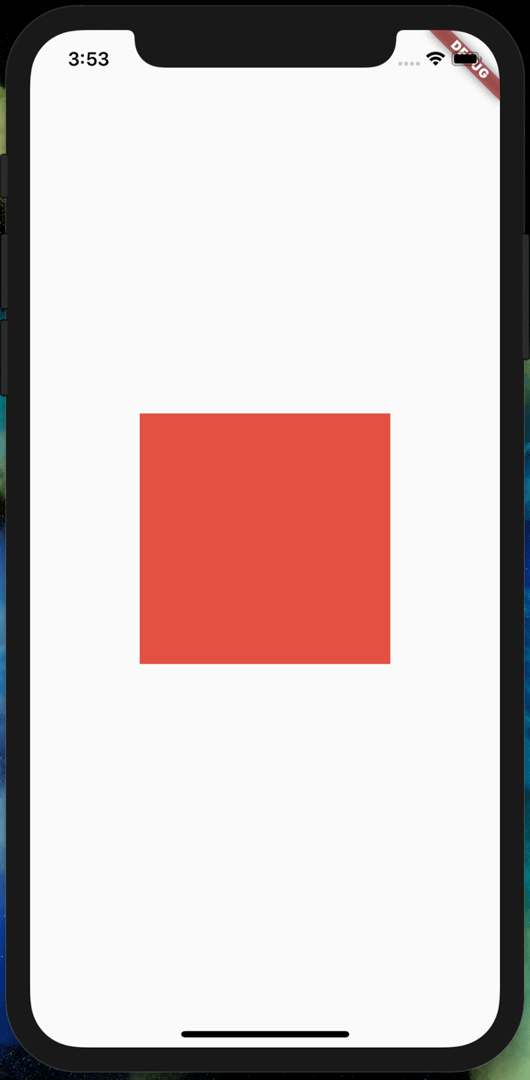
Very interesting square we have there. Let’s see if we can do something
with it.
Scaling using the matrix
Let’s try to scale (expand/contract) the square in X, Y, Z directions
and then all together.
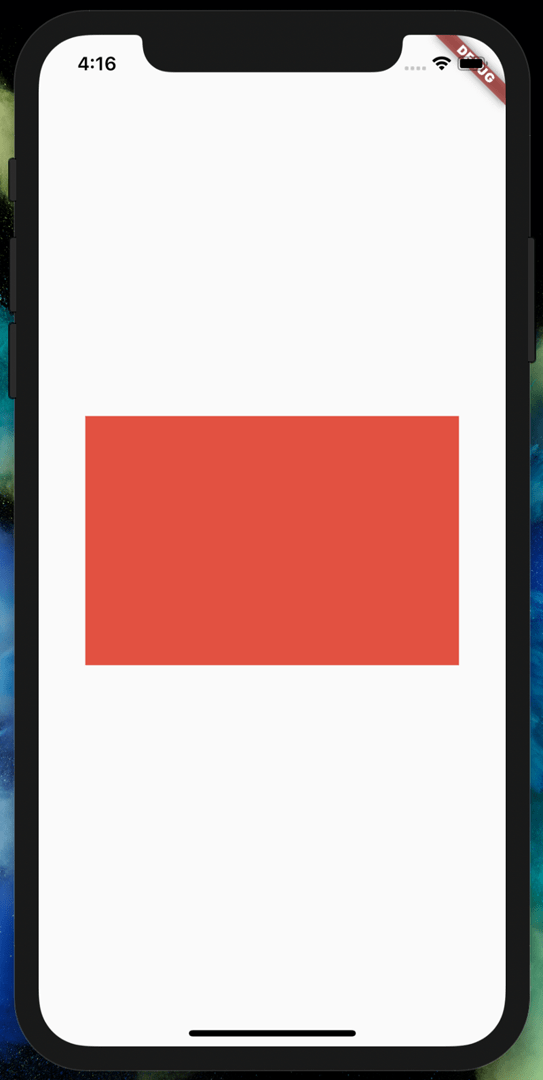
Scaling in X

To scale an object in the X direction (horizontal), change the (0,0)
value of the matrix with the scaling factor required.
Let’s try doing this. With a scaling factor of 1.5, our square becomes:
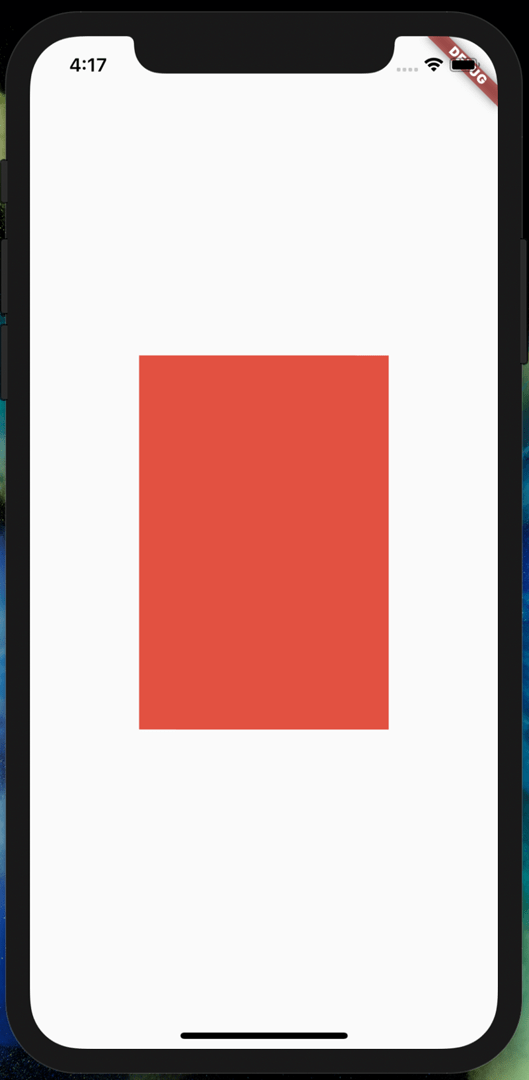
Scaling in Y

To scale an object in the Y direction (vertical), change the (0,0) value
of the matrix with the scaling factor required.
Let’s try doing this. With a scaling factor of 1.5, our square becomes:
Scaling in Z?
Theoretically, the value (2,2) will scale in the Z direction, with a
similar matrix.

Since this doesn’t apply to our 2D square, we’ll let it go.
Scaling in all directions
One way to scale in all directions is to just combine the ways above and
use it to uniformly scale our square. However, we can also use another
method:
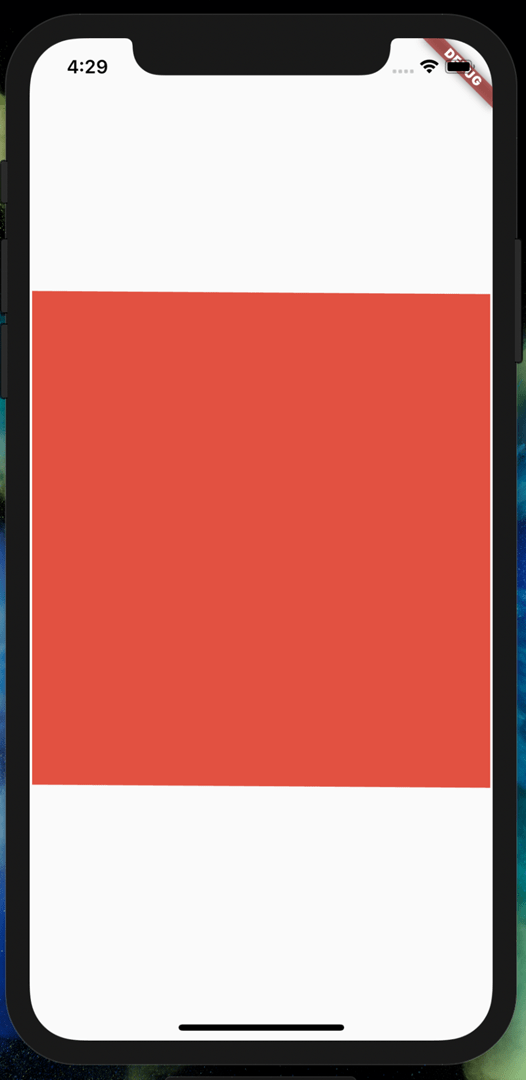
!

We can substitute the position (3,3) with 1 divided by the scale factor
we want to use. So if we want to make the square twice as big, we would
use 1/2, which is 0.5.
Here’s the square using 0.5 at (3,3):
Translation using the matrix

To translate in the X, Y or Z, directions, we can easily change the
bottom three values for X, Y and Z values respectively.
Important: The matrix given above represents the matrix in the code.
Since the actual Matrix4 goes by column-major format, X, Y and Z would
be at (0,3), (1,3) and (2,3) respectively.
Let’s take an X translation of 75 as an example:
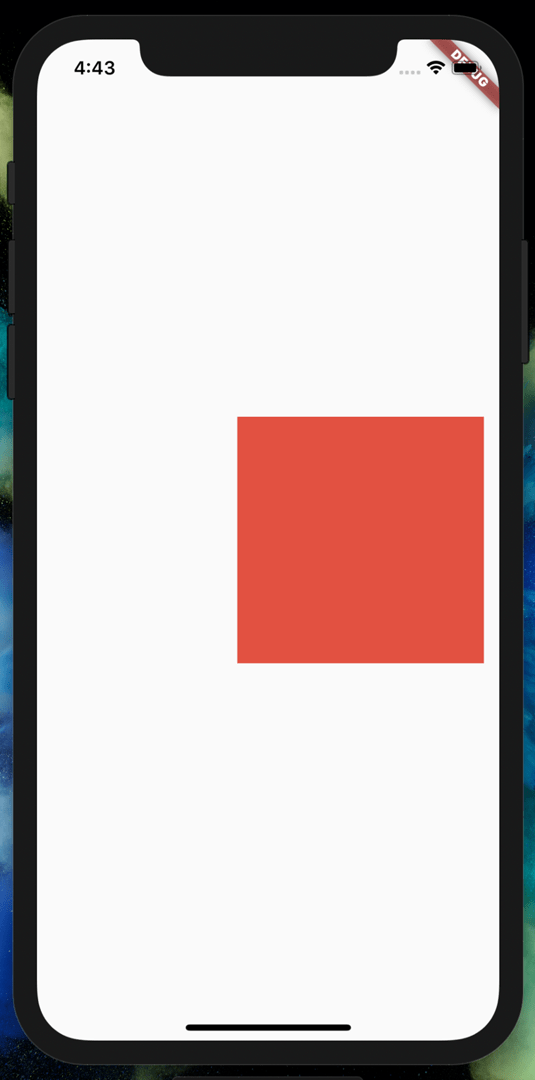
Rotation using the matrix
All things can’t be easy in life- hence, as simple as it was to scale
and translate objects with the matrix, rotation is no easy thing to
remember and something you would mess up on your math finals.
For rotation on around X axis:
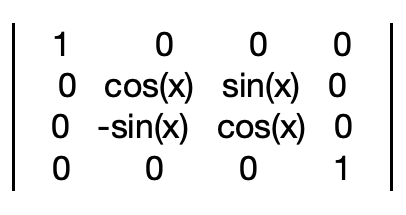
For rotation around the Y axis:
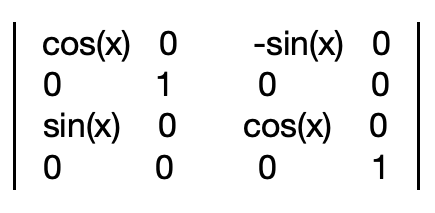
For rotation around the Z axis:
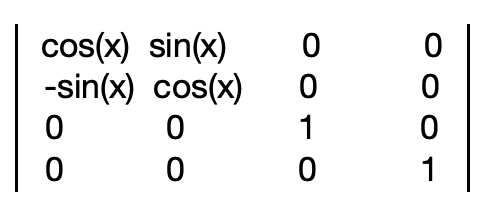
This may just explain why in the starter code we had
..rotateX***(*x*)***..rotateY***(*y*)***..rotateZ***(*z*)***
and not a manual implementation of angles and further matrix
multiplication.
Perspective Transformations
Perspective transformations modify lengths over positions along an axis.
The most common use of this is to give the user a sense of depth — the
way railway tracks look wide where you’re standing but get shorter and
shorter as you look farther. In this context, the side of the square
closer to us should look bigger and the one away from us should look
smaller.
Let’s take a look to better understand this. Currently, when we play
around with the square with the starter code, it looks like this:
There is no perception of depth when the square rotates. We can fix this
using perspective transformation. To enable depth perception in the Z
direction, we need to set this value in the matrix in the code-

You may have seen other tutorials using this line:
..setEntry***(***3, 2, 0.001)
This reduces lengths when the object goes farther away and increases
them when they come nearer.
Let’s set the z value to 0.002 and see what happens to our square.
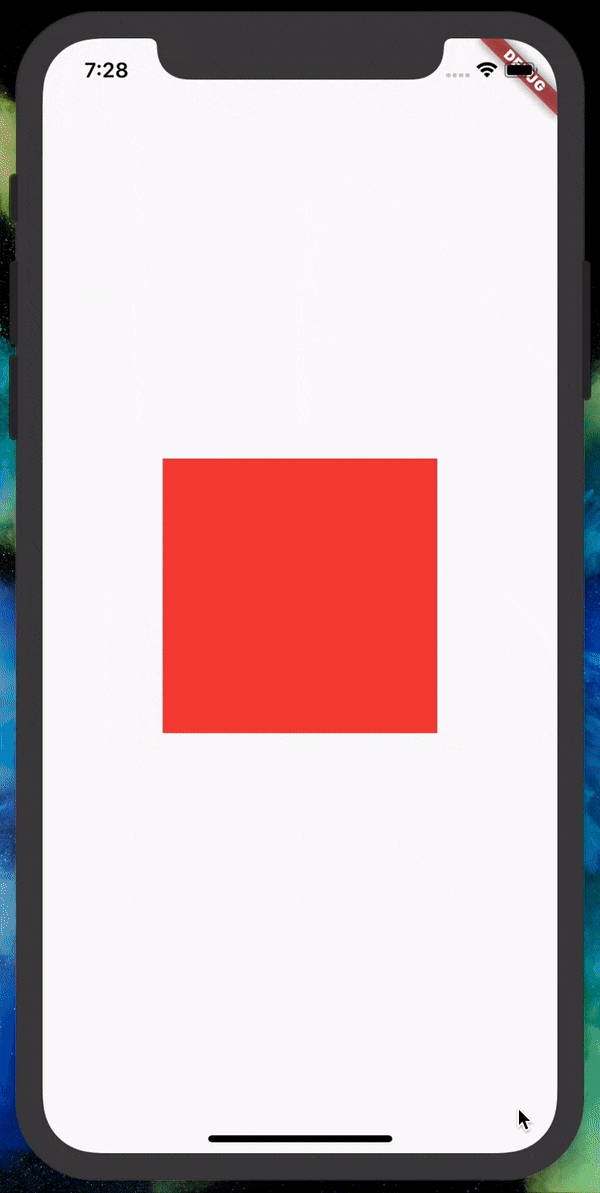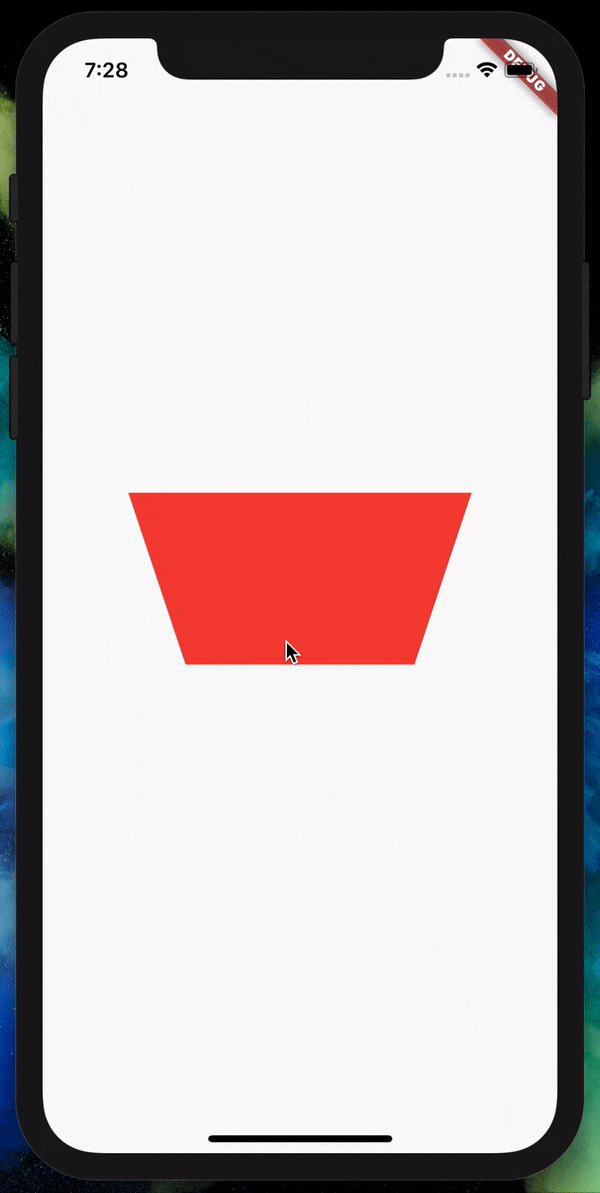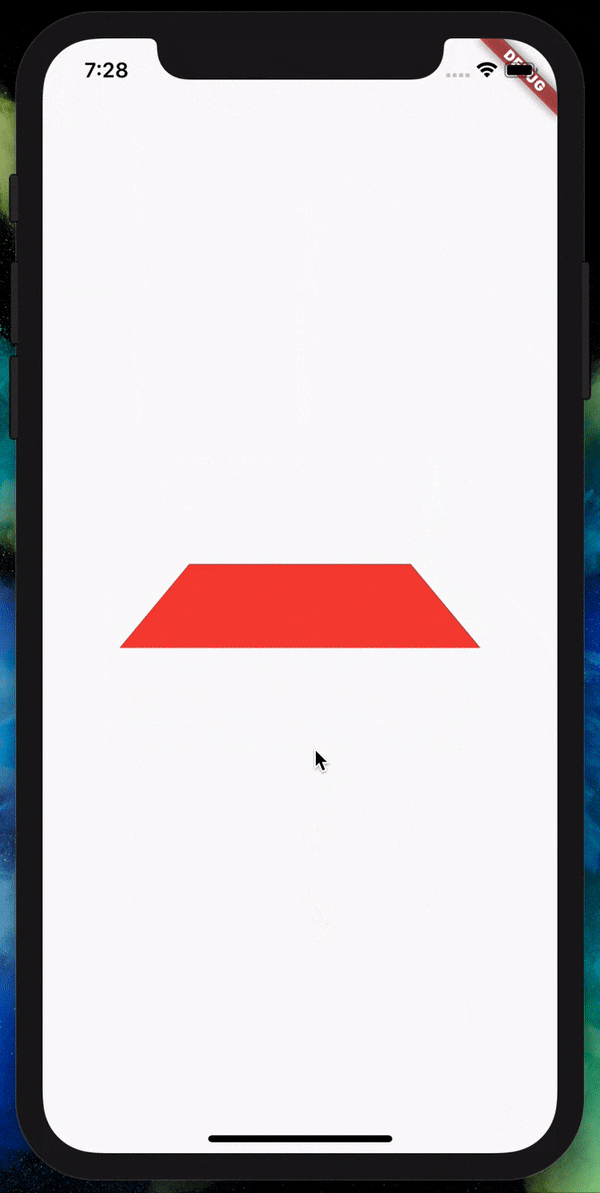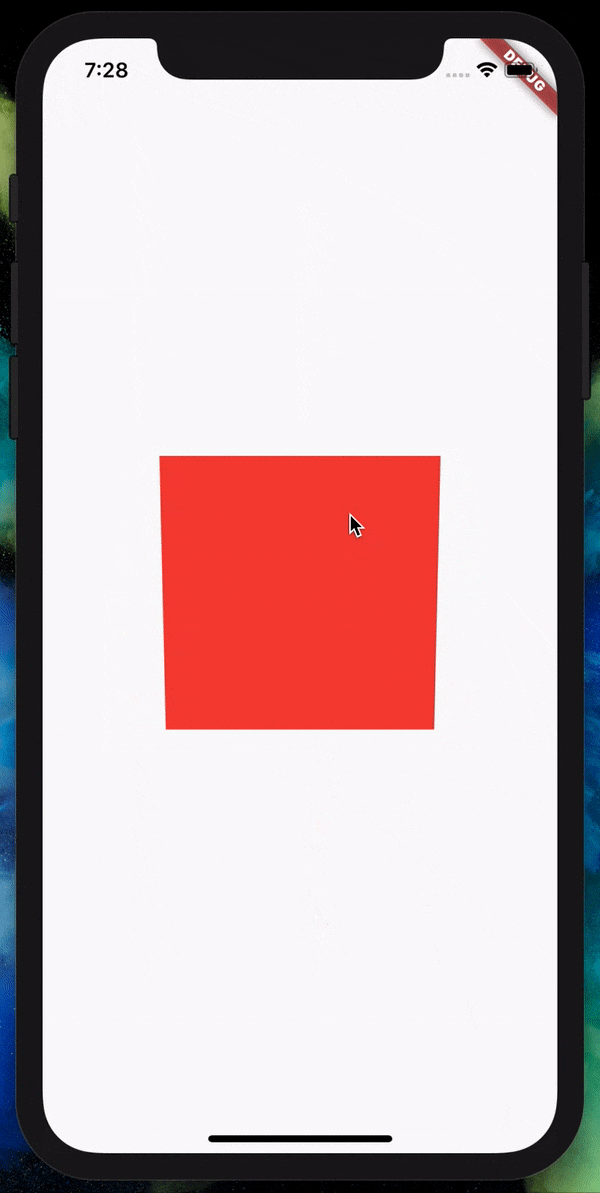
We can now see the difference and the nearer side becomes bigger and the
farther side becomes smaller. A higher value will give a higher gradient
of length by distance.
But… that’s not it
If you noticed a symmetrical theme for all axes in this article, you may
be thinking “what about the two values above the depth perception value
for the Z axis”?
Similar to the Z axis, the other two values also work the same way.

Setting this value allows us to perceive distance along the X axis like
we did with the Z axis. While this isn’t necessarily the same effect,
this is still theoretically identical to the perspective transformation
done above.
Here, as position in the X axis increases, length of sides decrease,
something like this:

Similarly, for the Y axis:

Origin in computer graphics is at the top-left corner, hence, the Y
position increases as we go down. Therefore, length shrinks going down
since the Y value going down is “farther”.
Deven Joshi is a mobile developer (Flutter + Android) | Technical Writer | Speaker | #Hack19 Winner | AAD graduate. You can follow him on twitter @DevenJoshi7 and on GitHub



















Discussion about this post